一、题目详细分析

1. 问题核心描述

给定一个由1、2、3组成的队列（1=最高优先级，2=中等优先级，3=最低优先级），计算每个位置的“愧疚指数”——即该位置后面优先级比它更高的人数。

2. 核心考点

• 时间复杂度优化：题目中n的上限是200000（2e5），若采用“每个位置遍历后面所有元素”的暴力解法（O(n²)），会因超时无法通过100%数据，必须设计O(n)的线性时间解法。
• 反向遍历+计数器维护：利用“从后往前遍历”的思路，维护已遍历元素中高优先级的数量，避免重复计算。

3. 优先级与愧疚指数的对应关系

4. 解法思路

• 反向遍历：从队列最后一个元素向前遍历，因为当前元素的“后面元素”就是已经遍历过的元素。
• 计数器维护：
  • s1：记录已遍历元素中1的数量（最高优先级）；
  • s2：记录已遍历元素中2的数量（中等优先级）；
• 实时计算：遍历到每个元素时，根据其类型直接用计数器计算愧疚指数，再更新计数器（仅1和2需要更新，3不影响后续计算）。

二、代码逐行详细注释

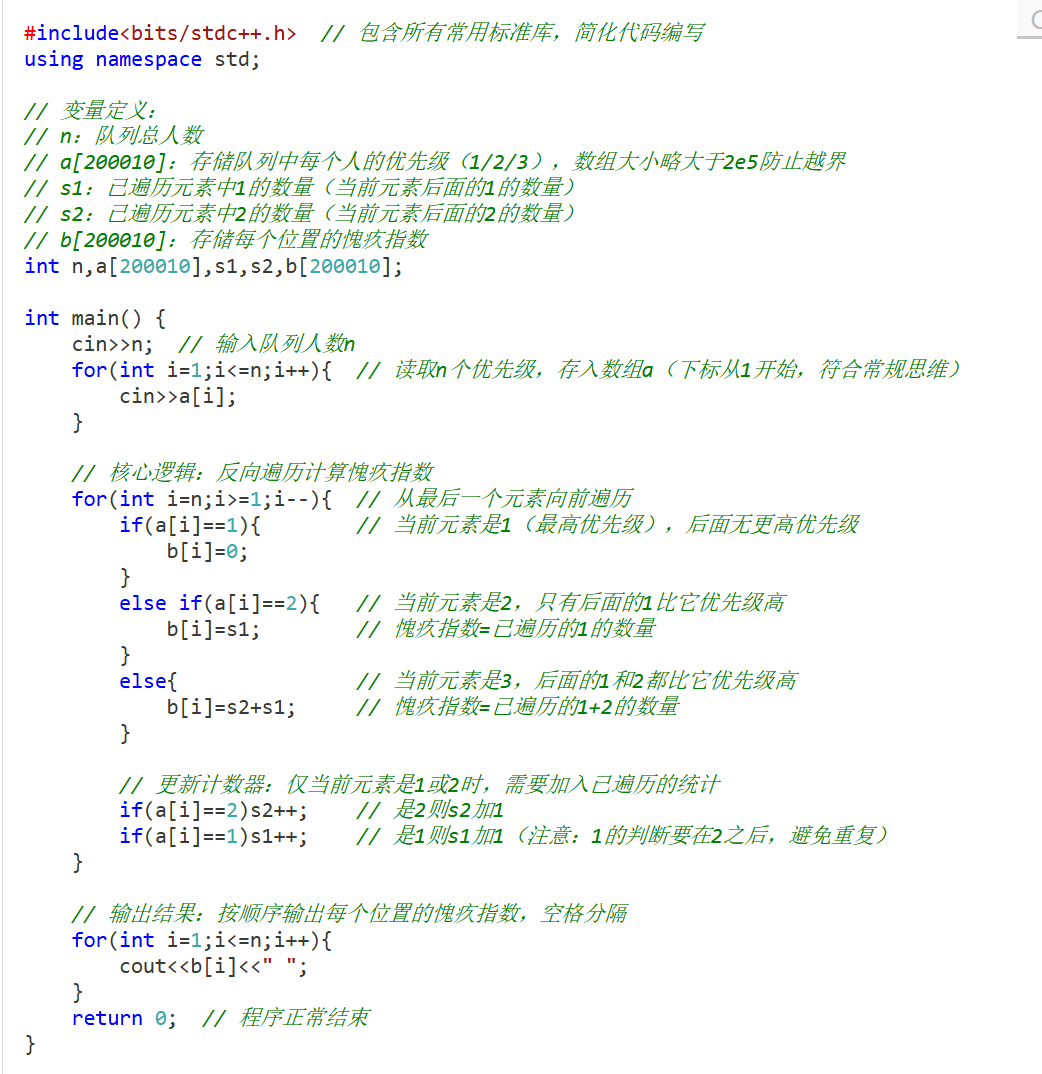
三、示例验证（输入：5 3 2 1 2 1）

我们通过手动模拟反向遍历过程，验证结果正确性：

最终b数组为[4,2,0,1,0]，与示例输出完全一致。

四、时间/空间复杂度分析

• 时间复杂度：O(n)。仅需两次线性遍历（一次输入，一次反向计算，一次输出），所有操作都是常数级。
• 空间复杂度：O(n)。主要消耗在存储数组a和b，空间大小与n成正比，符合2e5的数据规模要求。

该解法完美适配题目100%的数据范围，是最优的线性时间解法。