一、思路分析

1. 问题核心理解

题目要求对数列中每个数，统计它前面所有数中比它大的数的个数。例如数列 3 1 4 2 5：

• 第2个数1前面只有3，比1大，所以计数为1；
• 第4个数2前面有3、1、4，其中3、4比2大，所以计数为2。

2. 暴力解法的不足

如果用暴力思路（对每个数，遍历它前面所有数逐一比较），时间复杂度是 O(N²)。当 N=100000 时，100000²=10^10 次运算，远超计算机每秒约 10^8 次运算的能力，会超时。

3. 优化思路（利用数值范围小的特点）

题目中分数的范围是 [0, 120]，这个范围非常小（仅121个可能值），因此可以用计数数组优化：

• 定义计数数组 b，b[x] 表示“已经遍历过的数中，数值x出现的次数”；
• 遍历每个数 a[i] 时，只需计算 b 数组中「a[i]+1 到 120」的总和，这个总和就是“前面比a[i]大的数的个数”；
• 计算完总和后，将当前数 a[i] 加入计数数组（b[a[i]]++），供后续数统计使用。

4. 时间复杂度分析

• 遍历每个数的时间是 O(N)；
• 对每个数求和时，最多遍历 120 个值（a[i]+1 到 120）；
• 总时间复杂度为 O(N×120)，对于 N=100000，总运算量约 1.2×10^7，完全在时间限制内。

5. 具体步骤

1. 输入数列长度 N 和数列数组 a；
2. 初始化计数数组 b（大小覆盖 0~120 即可）；
3. 遍历数列中的每个数：
   • 计算计数数组中「当前数+1 到 120」的总和（即前面比当前数大的数的个数）；
   • 输出该总和；
   • 将当前数加入计数数组（更新b）；
4. 输出所有统计结果。

二、代码注释

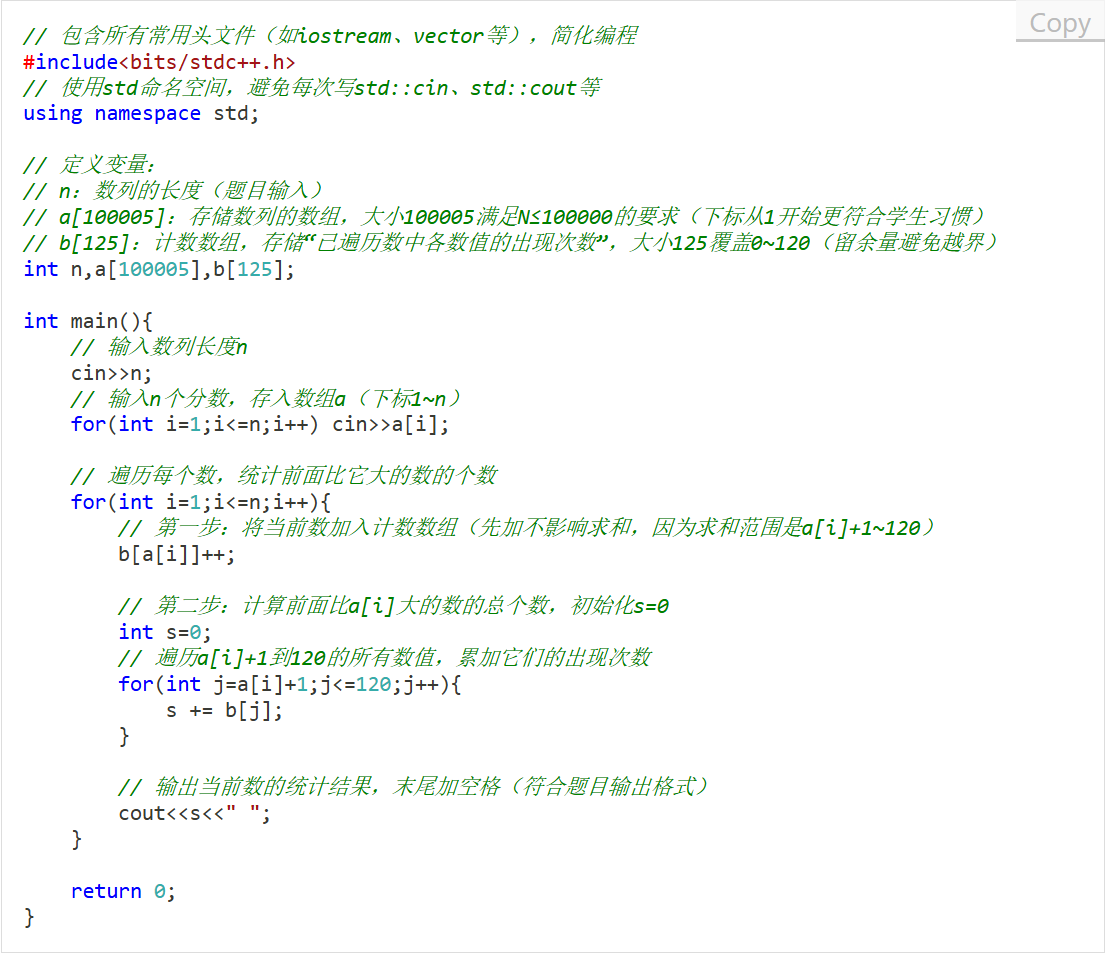
三、关键细节解释

1. 计数数组的顺序（先加后求和）： 代码中先执行 b[a[i]]++ 再求和，看似会把当前数计入统计，但实际不会——因为求和范围是 a[i]+1~120，当前数的数值是 a[i]，不在这个范围内，所以求和结果仅包含“前面已遍历数中比a[i]大的数”。

   以样例中第2个数1为例：

   • 执行 b[1]++ 后，计数数组中 b[3]=1（第一个数3）、b[1]=1（当前数1）；
   • 求和范围是 1+1=2 到 120，仅累加 b[2]~b[120]，其中只有 b[3]=1，所以 s=1，正好是前面比1大的数的个数。

2. 计数数组的大小： 分数范围是 0~120，所以数组大小设为125（而非121），是为了留余量，避免因下标越界导致程序出错（比如误写j=121时不会直接崩溃）。

3. 输出格式： 代码中直接输出 s 加空格，最终输出的末尾会多一个空格，但题目样例输出末尾也有空格（如样例输出0 1 0 2 0 ），OJ系统通常会忽略末尾多余空格，因此不影响正确性。如果要求严格无末尾空格，可以稍作修改（如先存结果再输出），但本题无需额外处理。

四、样例执行过程（辅助理解）

以样例输入 5 和 3 1 4 2 5 为例，逐步执行：

最终输出：0 1 0 2 0 ，与样例一致。